I came across this linkedin blog [How are negative numbers stored in binary?] [How the negative numbers are stored in memory? ] . These blogs provoked a related question : Why are 2's complement necessary at first place and why such systems are also not used for the quotidian Decimal system ?
Negative numbers has alwyas been difficult to undertand reason being its vicarious nature - when your friend lends you green dollars you can touch it, feel it, grasp it, but when he asks back you cannot really "see" any money, unless you press hard on your memory. The negative number are particularly recondite when it comes to how computer deals with this "negativity".
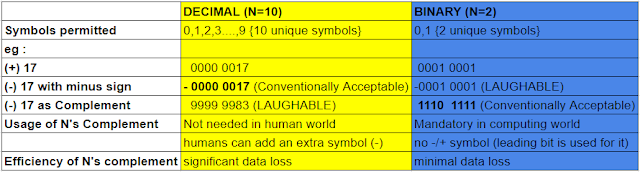
Let's revisit DECIMAL SYSTEM :
* only symbols, we call digits, permitted are : 0 to 9 (i.e. Ten symbols)
* we can represent all WHOLE Numbers (0,1,2,3...∞) using only these 10 symbols and their infinite jumbling combinations. (read Permutaions & Combinations).
At this point, Primates had no idea about what "-54" meant ? They logged informations like "The bald Primate owes 50 rice grains to the hirsute Primate ". But as much water has flowed under the bridge some primate suggested why not replace "owed" with yet another symbol with, say, "-".
* Therefore, inorder to represent INTEGERS (-∞,...-3,-2,-1,0,1,2,3 ...) we agreed to use an additional symbol "-"
So, the Decimal system(0-9) is easy because we have made it easier by borrowing extra symbol of (-)ve.
Before we strike the pith of the blog title, bear me to answer this qustion :
How could we have written/represented negative numbers if you were not permitted to use an extra symbol like "-" ?
Let me rephrase question : "How will you write -7 without using (-) symbol in decimal system?" [Constraint: you can use any digit (0-9) for maximum 4 times as in 8764]
(why I have limited to 4 digits in this excercise? Because unlike when wrting on paper, in computer the size is limited based on data type - for example, an integer is stored in 32 bits)
Propsed Solution:
We have to find B such that A + B = 0
A = 7 = 0007 (represented as 4 digit)
Step I : now take 9's complement* = 9999-0007 = 9992 [DEFINITION: 9's complement of A = highest number possible - A]
Step II: Add 1 : 9993 (This is B i.e. -7) [10's complement of A]
Lets verify : A + B = 0007 + 9993 = 1 0000 = 0000 (discard the leading 1 because we can only use 4 digits)
Agreeing to Agree on somethings is at the cornerstone of any system we devise to ease our transactions. What we have implictly agreed above is that if the left most symbol will be of highest value out of 10 symbols(i.e. 9) then it will represent negative number. And if the left most symbol is of the lowest value out of 10 symbols (i.e 0) then it will represent positive number.
Then obvious counter question will be : how can we represent a number greater than 8999 , say 9000 using above agreement? Won't this 9000 be actually representing : positive 1000
Let A = 1000
I. 9999 - 1000 = 8999 (9's complement of 1000)
II. 8999 + 1 = 9000 (10's complement of 1000)
The answer is no, 9000 = -1000. Because for 4 spaces we cannot represent (positive) number greater than 8999. Why? Because of our prior tacit agreement about TRADEOFF between RANGE & SIGN.
either, you can represent 10 thousand WHOLE Numbers from 0000 to 9999
or, you can represent 999 negative integers(9001to999) & 999 positive integers(0001to0999) and one zero (9000 or 0000). Total numbers = 1999 The leading number will act as sign indicator. Such drastic fall in range because one space, the leftmost space, which could have hold 10 information is used to present only two infromation (+/-).
Now, Enter the world of BINARY SYSTEM :
* only two symbols: 0 and 1 are permitted.
In the Binary system, at the machine level we dont have luxury of adding (-ve) symbol. Everything is black(0) & white(1) - either 0 or 1. (unless you are using quantum computer).
So early programmers have devised an igenious way(already explained above) to overcome this scarcity.
A = 7 is represented in binary (8-bit) as 0000 1101
Step I : 1's complement of A : (highest no possible - A) = 1111 1111 - 0000 1101 = 1111 0010
Step II: 2's complement of A : 1's complement + 1 = 1111 0010 +1 = 1111 0011
Verify : 0000 1101 + 1111 0011 = 1 0000 0000 = 0000 0000 (leading 1 will be discarded for 8-bit)
PS: the range loss in binary system is much lesser compared to decimal system . Hence it made sense to use above representation in binary systems.
Capacity reducation for 4 spaces if we store negative numbers :
1. Decimal system : 10,000 --> 2000 (1000 postive , 1000 negative) : 5x loss
2. Binary system : 16 (0000 to 1111) --> 15(1111/-7 to 0 to 0111/+7) - hardly any loss
Thanks.